Inada conditions

In macroeconomics, the Inada conditions (named after Japanese economist Ken-Ichi Inada)[1] are assumptions about the shape of a production function that guarantee the stability of an economic growth path in a neoclassical growth model.

The six conditions for a given function f(x) are:

  1. the value of the function f(x) at 0 is 0: f(0)=0
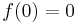
  2. the function is continuously differentiable,
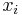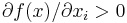  3. the function is strictly increasing in x_{i}: \partial f(x)/\partial x_{i}>0,
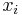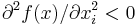  4. the second derivative of the function is decreasing in x_{i} (thus the function is concave): \partial^{2} f(x)/\partial x_{i}^{2}<0,
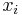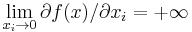  5. the limit of the first derivative is positive infinity as x_{i} approaches 0: \lim_{x_{i} \to 0} \partial f(x)/\partial x_i =%2B\infty,
  6. the limit of the first derivative is zero as 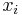x_{i} approaches positive infinity: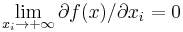 \lim_{x_{i} \to %2B\infty} \partial f(x)/\partial x_i =0

It can be shown[2] that the Inada conditions imply that the production function must be asymptotically Cobb–Douglas.

In stochastic neoclassical growth model if the production function does not satisfy the Inada condition at zero, any feasible path converges to zero with probability one provided that the shocks are sufficiently volatile.[3]

References

  1. ^ Inada, Ken-Ichi (1963) "On a Two-Sector Model of Economic Growth: Comments and a Generalization," The Review of Economic Studies, 30(2): 119-127
  2. ^ Barelli, Paulo and Samuel de Abreu Pessoa (2003) "Inada Conditions Imply That Production Function Must Be Asymptotically Cobb-Douglas" Economics Letters 81(3) 361-63
  3. ^ Takashi Kamihigashi (2006) "Almost sure convergence to zero in stochastic growth models", Economic Theory (Springer), 29(1), 231-237